Leveraging Smooth Latent Spaces for Video Generation

If you are interested in Generative Adversarial Networks (GANs) or Autoencoders, you've probably come across pictures like this one:

What you see here are images generated by interpolating in latent space. On a very high level, imagine the left- and rightmost pictures as your originals, then all images in-between are just a blend of the young women and the middle-aged man. To better understand how this blending actually works, let's first have a look into what a latent space is.

The above sketch shows the abstract structure of a GAN. Let's have a look a the elements: First, we have our latent vector. You can just picture it as a vector of random real numbers for now. The Generator is a Neural Network that turns those random numbers into an image that we call Fake Image for now. A second Neural Network, the Critic, alternately receives a generated, fake image and a real image from our dataset and outputs a score trying to determine whether the current image is real or fake.
Essentially, the Generator and the Critic compete while a GAN is trained. The Critic continuously learns to tell real images apart from generated images, the Generator tries to fool the Critic and thus produces more and more realistic images.
What's the deal with the latent vector though? We don't want our generator to always produce the same image. In a perfect world without any training issues and without that nasty phenomenon we call Mode Collapse, every combination of numbers in our latent vector produces a different image when fed through the generator. We can then sample a random latent vector whenever we want a new image.

Let's get back to our interpolated faces from the start. Researchers have gotten pretty good at achieving smooth latent spaces. More abstractly, this means that almost every latent vector produces a different, but realistic image when fed through the trained generator network. They also realized that different entries in the latent vector influence different aspects of the image. Take faces as an example: If your latent vector has 100 entries (so-called dimensions of latent space), it's likely that one of them exclusively influences hair color. If you were to generate faces from this vector and only change your hair-color dimension, the generated faces will be almost identical, but the hair colors would differ.

The same idea is used for interpolating between faces. First, we generate two random latent vectors, send them through our generator and out come two different faces: The young lady and the middle-aged man. Now picture those latent vectors as points in latent space. The figure above shows linear interpolation in 3.dimensional space: We have two points, draw a line between them and generate new points at equidistant steps of the line. Our latent space has a lot more dimensions, but the principle stays the same: We calculate the formula for a line between the latent vector of the young women and the one of the middle-aged man and draw new latent vectors along the line. As we learned before, entries in the latent vectors stand for features of the faces, so all we need to do now is send our new samples through the generator network and voilà, we get faces with a gradual blend between the face characteristics of our young lady and our man.

Now that we know about the basics of latent vectors and GANs, we can finally get to the new stuff! Generating novel, realistic images is very impressive, but "dreaming up" never-before-seen videos is, kind of, the holy grail of using GANs. The problem with videos is that not only the individual frames have to look realistic, but you also need so-called temporal consistency, meaning that the concatenation of all your predicted frames has to look like a realistic video, especially with realistic movement of objects.
Many approaches exist for the challenge, but the countless interpolation images inspired us to try something new: What if we can train a GAN to develop a latent space so smooth that we can simply interpolate between two still images and generate so many frames in-between that we can build a whole video from it? We don't want random videos though, do we? We also want to influence what our video is about. Long story short, this is what we came up with:

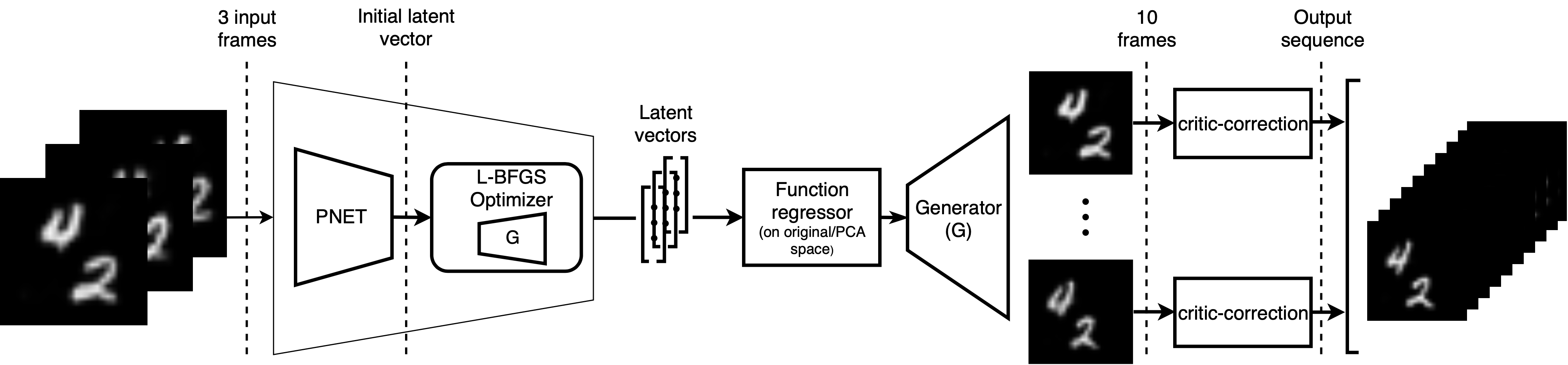
Looks complicated, right? Let's go through it step by step. To keep everything as simple as possible for now, we decided to use the Moving MNIST dataset, a collection of short video clips in which two handwritten numbers float around on a black background. First of all, we trained a GAN on individual frames of our dataset to get a generator that turns random latent vectors numbers into realistic images of two handwritten digits. As we only need the generator network for our pipeline, we discarded the critic.
The left half of our pipeline is responsible for conditioning, meaning we use it to define what our generated video will be about. Therefore, our input consists of an arbitrary number of images containing the same two digits at different locations. Eventually, we want to connect those input frames by a generated video.
We learned that we can generate new images from latent vectors, so now we face the inverse problem: How do we transform our input images into latent vectors that we can later use for our video generation?
Naively, we could just try out a lot of different random vectors, send them through our generator and check whether the images are similar to what our input looks like. Once we find it, we would know that this specific random vector must be the latent representation of our image. Obviously, with a latent space of 256 dimensions, that would take forever, so we make use of numerical optimization. The L-BFGS optimizer minimizes the difference between our input image and the image generated by a latent vector by continuously adapting the entries in the latent vector, starting from an initial guess. To do that, it needs a first derivative. Luckily, our generator is a fully differentiable neural network, so we can use the network's backward pass to calculate our derivative for the L-BFGS optimizer.
In many cases, this numerical optimization finds a pretty good match in latent space for our input image. Unfortunately, numerical optimization is heavily dependant on initialization, so sometimes it just returns absolute rubbish. What do we usually do when well-established methods fail? You're right, we just throw some more deep learning at the problem and hope for the best! In this case, we trained P-NET, which stands for projection network. The fully connected neural network's job is to predict the most probable latent vector given an input image. To calculate the network's loss during training, we turn the predicted latent vector into an image using the generator and calculate the image similarity of that image to the initial input.

We tried out different combinations of P-NET and numerical optimizers and concluded that we get the best back-projections of input images into latent space by initializing an L-BFGS solver with the output of P-NET, which in turn gets our conditioning image as input.

Now that we've got our input images mapped into our latent space nicely, we need to make a video out of them. We learned about interpolation earlier, but now that we've possibly got more than two points to draw a line between, we use regression instead of interpolation.

As you can see above, the idea is very similar, the is simply calculated as a "best approximation" of all points instead of intersecting with the points directly. We also experimented with using higher-order polynomials instead of lines, but the results turned out best with a simple first-order line. This 256-dimensional line through latent space is the first glance at our generated video (it's still a video in latent space, so not very readably for humans...).
To generate our actual video frames from the line, we have to discretize. Similar to the interpolation problem of images, we simply sample a lot of points from our line. All of those points will later produce one frame of our video.

One problem of latent spaces is the fact that you don't know how many dimensions you need before trying it out. You want to have enough dimensions to capture all your image features, but too high-dimensional latent space leads to an unstable regression problem because all of the dimensions are noisy by nature. We discovered that Principal Component Analysis (PCA) alleviates that problem. Let's have a quick look at what PCA is:

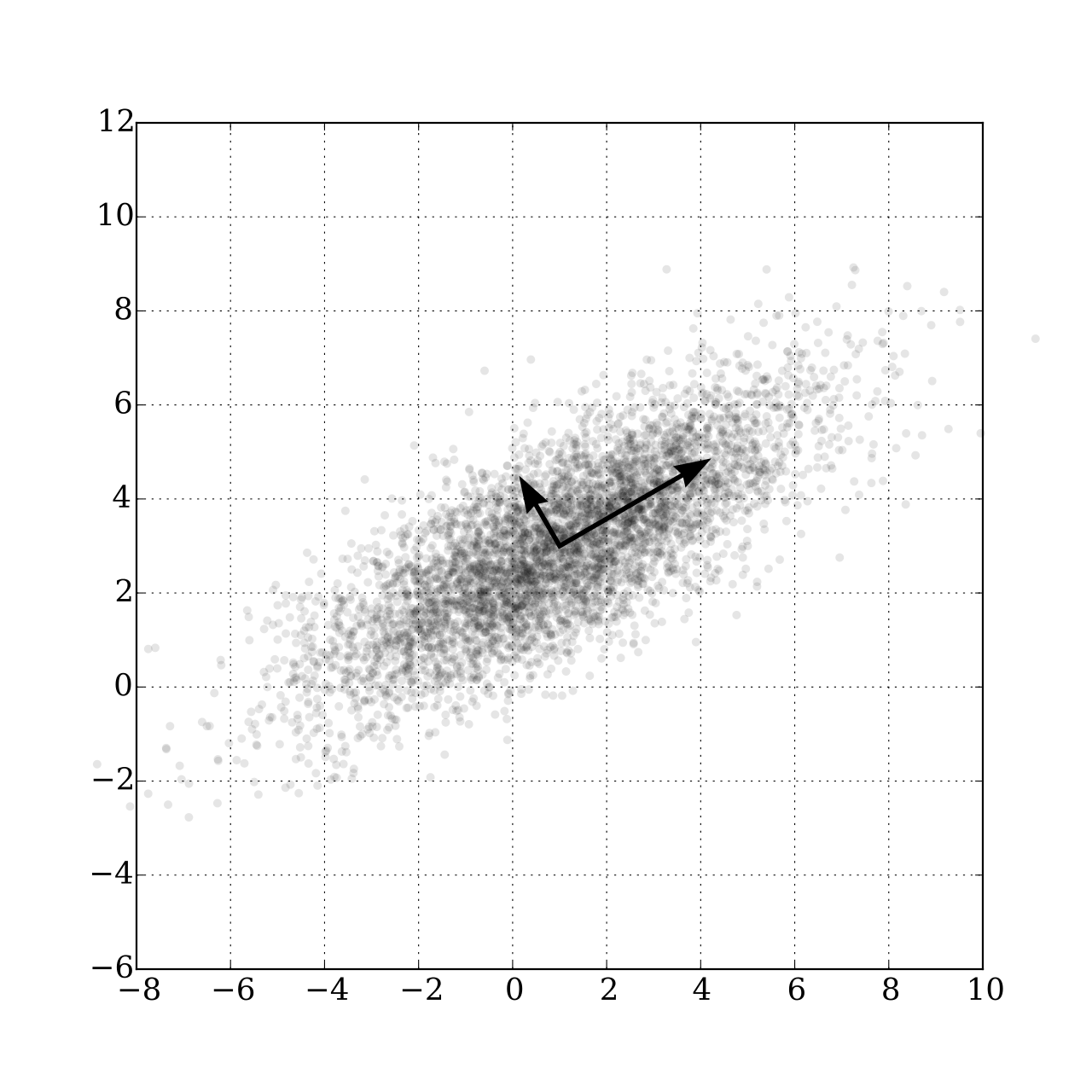
As you can see, you need two coordinates to specify the location of the points above. If you place your coordinate system as drawn in black, though, your new x coordinate specifies your point location pretty well! This means by finding the right coordinate system, you can reduce the dimensionality of your data to only the important, "principal" dimensions and discard all the excess noise. People usually choose their new axes in a way that retains 95 or 99% of your initial variance in data.
We found that applying PCA to our latent vectors, then regressing a line in principal space, sampling from this lower-dimensional line and transforming the sampled points back into our initial space improves the resulting videos a lot if the latent space is very high-dimensional. You can think of this as only changing the most important aspects in a video from one frame to another. You want your numbers to move, so there will be a lot of variance in the dimensions that correspond to the position, but the exact appearance of the digits only changes due to noise, so those changes should be and are filtered out by regressing in PCA.

At this point, all we have to do to transform our latent video into an actual video is to feed all those sampled latent vectors through our pre-trained generator network to obtain individual video frames. If we concatenate the frames into a video clip, we already see numbers floating around, which means out pipeline seems to work! We did, however, notice that the digits do still change their appearance quite vividly. This is because the whole process is quite prone to noise, especially if the generator network is not trained to perfection (which is always the case in deep learning), small noise in the latent vectors can lead to very visible changes in the resulting video frames. We came up with one last optimization technique to improve our generated videos: critic-correction.
Remember when I told you we can discard our critic from our GAN training because we only need the generator? Well, at this point, we realized that the critic is very useful to have around, after all, so we went back to the trash can of our cloud and brought it back to life. The critic has to assess how real an image looks, so we decided to make use of its ability to do so. We take the frames that our generator produces and pass them through the critic to assess their "realness". We then perform a few steps of gradient ascent, meaning we optimize the image to obtain a higher critic score. This changes the images to look more like two actual digits, meaning any strange artifacts and blurriness are removed. By choosing a small step size, we tried to ensure that the numbers aren't changed by the optimization. This optimization rests on the assumption that a clearly-written digit is closer to it's blurry and messed-up version than an entirely different digit. While there is no theoretical proof for this assumption, the results seem to confirm that it is sensible.

Finally, these are short videos that our pipeline generates if you supply 3 singe input images containing the same digits:

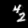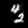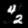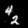
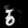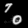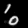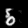
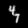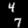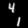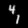
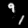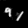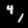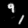
Pretty cool, right? You can see that the digits are smoothly moving through the frame. As you probably noticed, we still experience a bit of instability in the appearance of the digits and sometimes the number even changes, but all in all, we feel like it's a very good start. The main factor for improving the results is achieving a smoother latent space in the initial GAN training.
We are confident that existing trained GANs can utilize the pipeline we developed to generate high-quality videos and hope to see some results with more exciting content than moving numbers soon!

This turned out to be a pretty long blog post, but I hope you got the gist of our project and learned a lot on the way. If you have any questions, drop me a message! For technical details of our implementation, check out my GitHub Repo. Thanks for reading!